杨龙宇真棒！

谢谢你，杨龙宇~

这是一道非常难xxs都会做的题，巧妙的考察了二叉树。这里有道类似的题P1298 最接近的分数 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

我们先讲解一种数据结构Stern-Brocot Tree Stern-Brocot Tree (详见Stern-Brocot Tree - Achtoria - 博客园 (cnblogs.com))是一种人为构造生成,所有正有理数的树形结构，树上的每个节点与全体有理数（最简形式） ​构成双射。

简单来说，这棵树是这样生成的：

首先由两个初始分数0/1和1/0 ,（后者虽然无定义但可视作∞这只是形式化的辅助） 每一次迭代考虑在任意两个相邻分数a/b,c/d之间插入一个分数：(a+b)/(c+d)构成一个新的序列， 如下图所示：

以1/1为根，以与左边的数生成的数为左儿子，与右边生成的数作为右儿子（已经在树上出现过的节点不连左右儿子）为了方便构造，我们将数上出现过的数平移下放构成序列（实际上这些数并不在 Stern-Brocot 树中），如下图所示：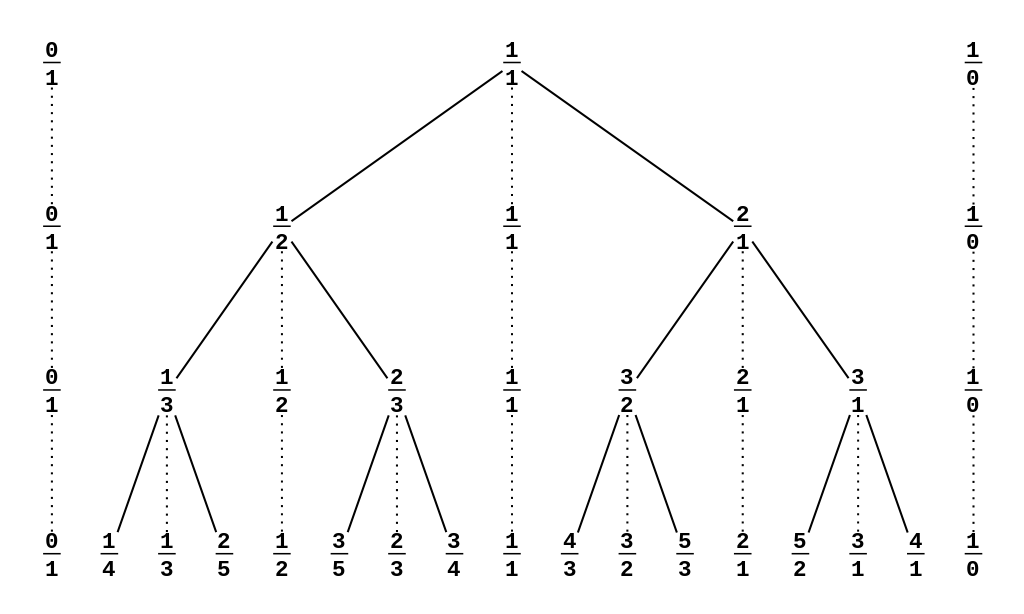

很明显这是一颗二叉查找树（Binary Search Tree），满足二叉查找树的性质： （1）若左子树不空，则左子树上所有的值均小于它的根节点的值；

（2）若右子树不空，则右子树上所有结点的值均大于它的根结点的值；

（3）左、右子树也分别为二叉查找树；

显然，深度越小的节点，分母与分子之和最小。基于这种贪心的思想，每次询问，我们按照二叉查找树的性质从上往下搜索这颗树，就可以在log n的时间复杂度搜索出答案。

请在luogu上关注我

#include<bits/stdc++.h>
#pragma GCC optimize(2)
//手动开O2 
using namespace std;
char ch;
inline int read(){//inline是内联修饰词,以空间换时间 
	register int ans=0;//这里的 register是存器修饰词会把变量尽量放入寄存器 
	while('0'>ch||ch>'9')ch=getchar();
	while('0'<=ch&&ch<='9')ans=(ans<<1)+(ans<<3)+(ch&15),ch=getchar();
	// ans=(ans<<1)+(ans<<3)与ans*=10等效 	
	//观察发现:数字的ASCII码5、6位都是1,数字至于后四位有关，所以按位与上15(00001111)或异或48(00110000)就可以消掉5,6位
	return ans;
}
void write(int ans){//快写 
	if(ans<10)putchar(ans|'0');//转换为ASCII码 
	else write(ans/10),putchar((ans%10)|'0');
}
struct frc{//定义分数的结构体 
	int a,b;//分母，分子 
	bool operator<(frc &x){//operator为重载运算符 
		return a*x.b<x.a*b;
	}
	frc operator+(frc &x){//这里的+并不是真正意义上的加法，而是方便书写用的 
		return {a+x.a,b+x.b};//{}可以直接用于结构体赋值但是如果有构造函数再用{}可能会报错 
	}
};
int main(){
	cin.tie(0);//这是个读入的优化，但是写了后cin和scanf不能同时用 
	read();//直接不需要n 
	int q=read();
	frc l,r,x,y,mid; 
	while(q--){//循环q次 
		l={0,1},r={1,0},x={read(),read()},y={read(),read()};
		while(1){
			mid=l+r;//计算出节点 
			if(y<mid)r=mid;//如果都在左侧，访问左子树 
			else if(mid<x)l=mid;//如果都在右侧，访问右子树 
			else break;	//左右之间就是答案 
		}
		write(mid.a+mid.b),putchar('\n');//输出答案 
	}
	return 0;
}

诚信做题，请勿抄袭。 谢谢